1. Skalar dapat didefinisikan secara lengkap oleh bilangan tunggal dengan satuan yang sesuai.Skalar juga dapat diartikan sebagai bilangan yang memiliki nilai satuan tanpa arah.
Contoh Skalar:panjang,luas,volume,massa,waktu

2. VEKTOR adalah bilangan yang memiliki nialai satuan dan memiliki arah.


2. VEKTOR adalah bilangan yang memiliki nialai satuan dan memiliki arah.
Contoh Vektor:gaya,kecepatan,percepatan
Misal:Kecepatan 10km/jam ke arah utara.
Angin yang bertiup ke timur laut sebesar 20 knot.
Representasi Vektor:
Vektor dapat direpresentasikan secara grafis,dengan garis yang ditarik sedemikian sehingga:

- Panjang garis menandakan besar vektor.
- Arah garis(ditunjukkan dengan mata panah)menandakan arah vektor.
contoh soal dan prmbahasan:
1. Ditentukan 2 buah vektor F yang sama besarnya. Bila perbandingan antara
besar jumlah dan besar selisih kedua vektor sama dengan √3, tentukan
besar sudut yang dibentuk oleh kedua vektor! (Sumber Soal : SPMB)
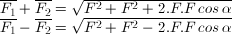
Perbandingan jumlah dan selisihnya adalah √3 sehingga:
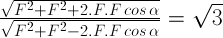
Kuadratkan ruas kiri dan kanan
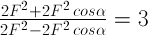
Kali silang :
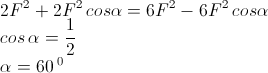
Pembahasan
Jumlah dan selisih kedua vektor masing-masing adalah:
Perbandingan jumlah dan selisihnya adalah √3 sehingga:
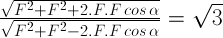
Kuadratkan ruas kiri dan kanan
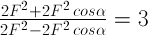
Kali silang :
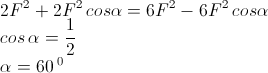
hasil karya mind mapping:










